Rectificación de media onda no controlada con carga inductiva y fuente de continua

En esta página encontraras un estudio del funcionamiento de un circuito rectificador de media onda con controlado con una carga resistiva-inductiva y fuente de continua.

Objetivos

El objetivo principal va a ser el estudio de la rectificación de una señal de corriente alterna en otra señal lo más continua posible.

Obtendremos los valores y las siguientes gráficas del circuito de rectificación de media onda onda no controlada con carga inductiva y fuente de continua:

*La tensión en el diodo D.

*La tensión en la fuente de continua y en la de alterna.

*La intensidad en el diodo D.

*La intensidad media en el diodo D.

*La intensidad eficaz en el diodo D.

*El ángulo de comienzo de la corriente.

*El ángulo de extinción de la corriente.

*El valor del factor de potencia del circuito.

*El valor de la potencia media disipada por la fuente de continua.

Materiales didácticos

Lecciones

Rectificación no controlada de media onda no controlada con carga inductiva y fuente de continua

Primero vamos a construir nuestro circuito:

Como podemos observar en el dibujo, tenemos los siguientes elementos:

Una fuente de continua $V_{cc}$ cuyo valor es de 10 Voltios.

Una bobina$L$ cuyo valor es de 50 milihenrios.

Un diodo 1N4148 al que llamaremos$D$

Una fuente de alterna$V_s$ cuyo valor es 30 Voltios, y de frecuencia 50 Hercios

La fuente de alterna obedece a esta ecuación:

$V(wt)=V_{cc}\cdot sen(wt)$

El circuito se puede definir por la siguiente ecuación:

$V_m\cdot sen(wt)=L\frac{di}{dt}+V_{cc}$

Para obtener la solución de este circuito vamos a obtener la intensidad que circula por él, por lo que vamos a pasar la fórmula anterior a formato angular:

$V_m\cdot sen(wt)=L\frac{dwi}{dwt}+V_{cc}$

Si despejamos de la ecuación la intensidad:

$di=(\frac{V_m}{Lw}\cdot sen(wt)-\frac{V_{cc}}{Lw})dwt$

Si integramos esta ecuación para los valores en los que circula intensidad por el circuito:

$i(wt)=\underset{a}{\overset{b}{\int }}(\frac{V_m}{Lw}\cdot sen(wt)-\frac{V_{cc}}{Lw})dwt$

Si hacemos la integral:

$i(wt)=\frac{V_m}{Lw}\cdot (cos(a)-cos(b))-\frac{V_{cc}}{Lw}\cdot (b-a)$

Siendo:

$w=2\cdot \pi \cdot f$

Y respecto a los límites de integración:

a =  α  $=arcsen(\frac{V_c}{V_m})$     (en radianes) 

Esta relación la obtenemos, ya que como sabemos,para que conduzca el diodo se tiene que dar la siguiente condición:

$V_m\cdot sen(wt)$ debe ser mayor que$V_c$

b : es un valor que hallaremos por tanteo.

Para hallar "b" , como conocemos "a" , vamos a igualar la ecuación a 0 , ya que como sabemos:

 i(β)=0 

Si sustituimos el "a" obtenido e iteramos con un valor para el ángulo "β" mayor que $\pi$ obtendremos el término "b" y entonces tendremos los límites de la integral.

Una vez hallados los límites de la integral, podremos obtener los siguientes valores de nuestro circuito:

El valor medio de la corriente:

$I_{AVG}=\frac{1}{T}\cdot \underset{a}{\overset{b}{\int }}[\frac{V_m}{Lw}\cdot (cos(a)-cos(wt))-\frac{V_{cc}}{Lw}\cdot (wt-a)]\cdot dwt$

El valor eficaz de la corriente:

$I_{RMS}=\sqrt{\frac{1}{T}\cdot \underset{a}{\overset{b}{\int }}[\frac{V_m}{Lw}\cdot (cos(a)-cos(wt))-\frac{V_{cc}}{Lw}\cdot (wt-a){]}^2\cdot dwt}$

Con estos valores podremos obtener:

Potencia absorbida por la fuente de continua:

$P=V_{cc}\cdot I_{AVG}$

Factor de potencia del circuito:

$fdp=\frac{V_{cc}\cdot I_{AVG}}{V_{sRMS}\cdot I_{RMS}}$

Siendo:

$V_{sRMS}$ es el valor eficaz de la fuente de alterna que será$\frac{V_m}{\sqrt{2}}$

Si volvemos al circuito antes dibujado,podemos observar las siguientes gráficas:

* La tensión en el diodo D:

* La tensión de la fuente de continua y alterna:

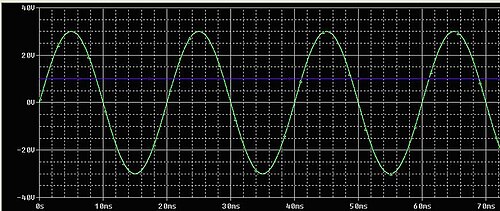Si ampliamos la gráfica,podemos ver cuando se cortan las dos tensiones:

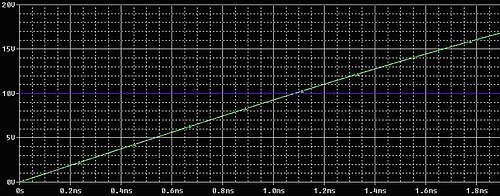Se cortan en 1,1 milisegundos.

* La intensidad en el diodo D:

Si ampliamos la gráfica,podemos ver cuando comienza y termina la intensidad:

La señal comienza a los 1,1 milisegundos.

La señal termina a los 13,5 milisegundos.

* La intensidad media en el diodo D:

La señal se estabiliza para un valor de 0,7 Amperios.

* La intensidad eficaz en el diodo D:

La señal se estabiliza para un valor de 1,04 Amperios.

Actividades

Ejercicios, pruebas de nivel de conocimiento, trabajos en grupo, u otras tareas. Todas ellas asociadas a sus respectivas lecciones.

• 1ª actividad.

EJERCICIO RESUELTO 1

• Tenemos un circuito rectificador de media onda no controlado con carga inductiva y generador de continua. Sabemos que el ángulo en el que la corriente empieza a circula por el diodo es de α=30º, que el generador de continua aporta una señal de continua de 25V y que la carga inductiva tiene un valor de 100mH. Calcular:

a)La amplitud de la fuente Vs

b)Potencia absorbida por la carga

c)Tensión media y eficaz en la carga

d)Factor de potencia del circuito

a) La amplitud de la fuente Vs:

Para que el diodo empiece a conducir la tensión senoidal debe superar a la tensión de Vcc. De manera que cuando la tensión Vs este en el ángulo α será igual que Vcc.

$V_s(\alpha )=V_m\cdot sen(\omega t)=V_{cc}$ $V_m=\frac{V_{cc}}{sen(\omega t)}$ $V_m=25/0,5=50V$

De aquí obtendremos el valor máximo de Vs, Vm = 50V

b) Potencia absorbida por la carga

Como se trata de una carga inductiva y un generador la potencia consumida por la carga será igual a la potencia absorbida por el generador, ya que si consideramos que la bobina es ideal esta no consumirá potencia, ya que toda la potencia absorbida será mas tarde entrega con el fin de mantener la corriente aun siendo negativa la tensión en el diodo. $P_{cc}=V_{cc}\cdot I_{0,AVG}$ Primero debemos calcular el valor de la corriente media. Para ello primero debemos lograr la corriente instantánea. $V_0=V_L+V_{cc}\to V_0=L\cdot \frac{di(t)}{dt}+V_{cc}\to V_{m}sen(\omega t)=L\frac{d\omega i}{d\omega t}+V_{cc}$ Ahora despejamos di. $di=(\frac{V_m}{L\omega }\cdot sen(\omega t)-\frac{V_{cc}}{L\omega })d\omega t$

Integrando obtendremos la expresión de la corriente instantánea.

$i(\omega t)=\underset{\alpha }{\overset{\omega t}{\int }}did\omega t=\underset{\alpha }{\overset{\omega t}{\int }}(\frac{V_m}{L\omega }\cdot sen(\omega t)-\frac{V_{cc}}{L\omega })d\omega t$

$i(\omega t)=[\frac{V_m}{L\omega }\cdot [cos(\alpha )-cos(\omega t)]+\frac{V_{cc}}{L\omega }\cdot (\alpha -\omega t)]$

De manera que la corriente será $i(\omega t)=[\frac{V_m}{L\omega }\cdot [cos(\alpha )-cos(\omega t)]+\frac{V_{cc}}{L\omega }\cdot (\alpha -\omega t)];\alpha <\omega t<\beta$

Para el resto i(ωt) = 0.

β será el ángulo de extinción de la corriente. Este ángulo lo podremos lograr igualando en ese punto la corriente a cero (i(β) = 0).

$i(\beta )=\frac{1}{2\pi }[\frac{V_m}{L\omega }\cdot [cos(\alpha )-cos(\beta )]+\frac{V_{cc}}{L\omega }\cdot (\alpha -\beta )]=0$

Iterando de esta expresión podemos obtener el valor de β, que será de β=3,8 rad .

Conociendo α y β, ahora podremos calcular el valor medio de la corriente.

$I_{0,AVG}=\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}i(\omega t)d\omega t=\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}[\frac{V_m}{L\omega }\cdot [cos(\alpha )-cos(\omega t)]+\frac{V_{cc}}{L\omega }\cdot (\alpha -\omega t)]d\omega t$

$I_{0,AVG}=\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}(1,78-1,59cos(\omega t)-0,79\omega t)d\omega t$

Integrando obtendremos el valor medio de la corriente.

$I_{0,AVG}=\frac{2,5}{2\pi }=0,4A$

Ahora podremos calcular el valor de la potencia absorbida por el generador de continua.

$P=V_{cc}\cdot I_{0,AVG}=25V\cdot 0,4A=10W$

c)Tensión media y eficaz en la carga

Para calcular la tensión media en la carga tenemos que integrar la expresión de la tensión entra α y β.

$V_{0,AVG}=\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}{V}_m\cdot sen(\omega t)d\omega t$

Integrando obtenemos que la tensión media es la siguiente.

$V_{0,AVG}=\frac{1}{2\pi }\cdot V_m\cdot (cos(\alpha )-cos(\beta ))=0,26\cdot V_m=13,18V$

La tensión eficaz la lograremos se la siguiente expresión.

$V_{0,RMS}=\sqrt{\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}{V}_m^2\cdot se{n}^2(\omega t)d\omega t}$

Para simplificar la expresión haremos el siguiente cambio trigonométrico.

$1=se{n}^2(\omega t)+co{s}^2(\omega t)$

$sen(2\omega t)=co{s}^2(\omega t)-se{n}^2(\omega t)$

Restando estas dos relaciones trigonométricas obtenemos lo siguiente.

$1-sen(2\omega t)=2\cdot se{n}^2(\omega t)$

Sustituyendo esto en la expresión para el cálculo de la tensión eficaz obtenemos lo siguiente.

$V_{0,RMS}=\sqrt{\frac{1}{2\pi }\cdot V_m^2\cdot \underset{\alpha }{\overset{\beta }{\int }}\frac{1-sen(2\omega t)}{2}d\omega t}$

Integramos y calculamos el valor eficaz de la tensión en la carga.

$V_{O,RMS}=\sqrt{\frac{V_m^2}{4\pi }\cdot [(\beta -\alpha )+(\frac{cos(2\beta )-cos(2\alpha )}{2}\left)\right]}=\sqrt{\frac{3,15\cdot V_m^2}{4\pi }}=25,03V$

d) Factor de potencia del circuito

Para calcular el factor de potencia usaremos la siguiente expresión.

$f.d.p.=\frac{P}{S}=\frac{P}{V_{S,RMS}\cdot I_{RMS}}$

Para poder calcular el factor de potencia primero deberemos lograr los valores de la tensión eficaz del generador de señal senoidal y el valor eficaz de la corriente que circula por el circuito.

$V_{S,RMS}=\frac{V_m}{\sqrt{2}}=35,35V$

Ahora calcularemos el valor de la corriente eficaz del circuito.

$I_{0,RMS}=\sqrt{\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}i(\omega t{)}^{2}d\omega t}=\sqrt{\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}(1,78-1,59cos(\omega t)-0,79\omega t{)}^{2}d\omega t}$

Integrando obtenemos el valor de la corriente eficaz que circula por el circuito.

$I_{0,RMS}=0,53A$

Ahora podremos calcular el valor del factor de potencia del circuito.

$f.d.p.=\frac{P}{V_{S,RMS}\cdot I_{RMS}}=\frac{10W}{35,35V\cdot 0,53A}=0,53$

EJERCICIO RESUELTO 2

• Partimos de un circuito rectificador de media onda no controlado con carga inductiva y generador de continua. El ángulo en el que la corriente empieza a circula por el diodo es de α=40º, el generador de continua aporta una señal de continua de 35V y que la carga inductiva tiene un valor de 50mH.

Calcular: a) La amplitud de la fuente Vs

b) Potencia absorbida por la carga

c) Tensión media y eficaz en la carga

d) Factor de potencia

a) La amplitud de la fuente Vs:

Para que el diodo empiece a conducir la tensión senoidal debe superar a la tensión de Vcc. De manera que cuando la tensión Vs este en el ángulo α será igual que Vcc.

$V_s(\alpha )=V_m\cdot sen(\omega t)=V_{cc}$ $V_m=\frac{V_{cc}}{sen(\omega t)}$ $V_m=35/0.643=54.43V$

Por lo tanto obtenemos el valor máximo de la señal de entrada:

$V_m=54.43V$

b) Potencia absorbida por la carga.

Considerando ideal la bobina diremos que no consume potencia alguna ya que la que consume en este momento mas tarde será aportada al circuito para evitar la interrupción de corriente, por lo tanto la potencia absorbida por el generador y la carga será exactamente igual. $P_{cc}=V_{cc}\cdot I_{0,AVG}$ Primero debemos calcular el valor de la corriente media. Para ello primero debemos lograr la corriente instantánea. $V_0=V_L+V_{cc}\to V_0=L\cdot \frac{di(t)}{dt}+V_{cc}\to V_{m}sen(\omega t)=L\frac{d\omega i}{d\omega t}+V_{cc}$ Ahora despejamos di. $di=(\frac{V_m}{L\omega }\cdot sen(\omega t)-\frac{V_{cc}}{L\omega })d\omega t$

Integrando obtendremos la expresión de la corriente instantánea.

$i(\omega t)=\underset{\alpha }{\overset{\omega t}{\int }}did\omega t=\underset{\alpha }{\overset{\omega t}{\int }}(\frac{V_m}{L\omega }\cdot sen(\omega t)-\frac{V_{cc}}{L\omega })d\omega t$

$i(\omega t)=[\frac{V_m}{L\omega }\cdot [cos(\alpha )-cos(\omega t)]+\frac{V_{cc}}{L\omega }\cdot (\alpha -\omega t)]$

De manera que la corriente será $i(\omega t)=[\frac{V_m}{L\omega }\cdot [cos(\alpha )-cos(\omega t)]+\frac{V_{cc}}{L\omega }\cdot (\alpha -\omega t)];\alpha <\omega t<\beta$

Para el resto i(ωt) = 0.

β será el ángulo de extinción de la corriente. Este ángulo lo podremos lograr igualando en ese punto la corriente a cero (i(β) = 0).

$i(\beta )=\frac{1}{2\pi }[\frac{V_m}{L\omega }\cdot [cos(\alpha )-cos(\beta )]+\frac{V_{cc}}{L\omega }\cdot (\alpha -\beta )]=0$

Iterando de esta expresión podemos obtener el valor de β, que será de β=3.82 rad .

Conociendo α y β, ahora podremos calcular el valor medio de la corriente.

$I_{0,AVG}=\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}i(\omega t)d\omega t=\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}[\frac{V_m}{L\omega }\cdot [cos(\alpha )-cos(\omega t)]+\frac{V_{cc}}{L\omega }\cdot (\alpha -\omega t)]d\omega t$

El valor medio de la corriente= 0.31 A

Ahora podremos calcular el valor de la potencia absorbida por el generador de continua.

$P=V_{cc}\cdot I_{0,AVG}=35V\cdot 0,31A=10.85W$

c) Tensión media y eficaz en la carga

Para calcular la tensión media en la carga tenemos que integrar la expresión de la tensión entra α y β.

$V_{0,AVG}=\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}{V}_m\cdot sen(\omega t)d\omega t$

Integrando obtenemos que la tensión media es la siguiente.

$V_{0,AVG}=\frac{1}{2\pi }\cdot V_m\cdot (cos(\alpha )-cos(\beta ))=13.56V$

La tensión eficaz la lograremos se la siguiente expresión.

$V_{0,RMS}=\sqrt{\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}{V}_m^2\cdot se{n}^2(\omega t)d\omega t}$

Para simplificar la expresión haremos el siguiente cambio trigonométrico.

$1=se{n}^2(\omega t)+co{s}^2(\omega t)$

$sen(2\omega t)=co{s}^2(\omega t)-se{n}^2(\omega t)$

Restando estas dos relaciones trigonométricas obtenemos lo siguiente.

$1-sen(2\omega t)=2\cdot se{n}^2(\omega t)$

Sustituyendo esto en la expresión para el cálculo de la tensión eficaz obtenemos lo siguiente.

$V_{0,RMS}=\sqrt{\frac{1}{2\pi }\cdot V_m^2\cdot \underset{\alpha }{\overset{\beta }{\int }}\frac{1-sen(2\omega t)}{2}d\omega t}$

Integramos y calculamos el valor eficaz de la tensión en la carga.

$V_{O,RMS}=\sqrt{\frac{V_m^2}{4\pi }\cdot [(\beta -\alpha )+(\frac{cos(2\beta )-cos(2\alpha )}{2}\left)\right]}=\sqrt{\frac{3,15\cdot V_m^2}{4\pi }}=27.5V$

d) Factor de potencia del circuito

Para calcular el factor de potencia usaremos la siguiente expresión.

$f.d.p.=\frac{P}{S}=\frac{P}{V_{S,RMS}\cdot I_{RMS}}$

Para poder calcular el factor de potencia primero deberemos lograr los valores de la tensión eficaz del generador de señal senoidal y el valor eficaz de la corriente que circula por el circuito.

$V_{S,RMS}=\frac{V_m}{\sqrt{2}}$

$V_{S,RMS}=\frac{55}{\sqrt{2}}=38.9V$

Ahora calcularemos el valor de la corriente eficaz del circuito.

$I_{0,RMS}=\sqrt{\frac{1}{2\pi }\cdot \underset{\alpha }{\overset{\beta }{\int }}i(\omega t{)}^{2}d\omega t}$

Es hacer la raíz de la ension calculada anteriormente

Integrando obtenemos el valor de la corriente eficaz que circula por el circuito.

$I_{0,RMS}=0,55A$

Ahora podremos calcular el valor del factor de potencia.

$f.d.p.=\frac{P}{V_{S,RMS}\cdot I_{RMS}}=\frac{10.85W}{27.5V\cdot 0,55A}=0,71$

• 2ª actividad.

EJERCICIOS PROPUESTOS

• El circuito rectificador de media onda con carga bobina-generador tiene un generador de alterna de 240 Vrms, con 60 Hz,la bobina presenta una inductancia de 0,2 H, y el generador de continua presenta 90 V. Calcular:

a)Angulo de entrada en conducción del diodo.

b)Potencia absorbida por el generador de continua.

c)Corriente Eficaz.

d)Factor de potencia.

Resultados:

a)α=0,2683 rad

b)Pcc=174,61 W

c)Irms=2,517 A

d)fp=0,289

• Un circuito rectificador de media onda con carga bobina-generador está compuesto por un generador de corriente continua de 76V. La bobina presenta una inductancia de 14 mH. El generador de alterna posee 160 Vrms, con una frecuencia de funcionamiento de 55 Hz.Calcular:

a)Expresión para la corriente.

b)Potencia absorbida por el generador de continua.

c)Factor de potencia.

Resultados:

a):$i(\omega t)=36,4658-33,07*cos(\omega t)-15,7(\omega t)$ para$\alpha \le \omega t\le \beta$ siendo$beta=3,88rad$

b)Pcc=544,92 W

c)fp=0,13

Referencias

ELECTRÓNICA DE POTENCIA (Daniel W. Hart)

http://www.datasheetcatalog.com/

Para encontrar el catálogo del diodo utilizado en este ejercicio visitar:

http://pdf.datasheetcatalog.com/datasheet/philips/1N4148_1N4448_4.pdf

Para aprender más sobre electrónica básica visitar este Canal de YouTube:

https://www.youtube.com/playlist?list=PLBe2MFU-GYFkdgnUbSlAKZpheeciicypL

Tutorial de electrónica básica general:

https://www.youtube.com/watch?v=px8qwS0ZHw8

Programa utilizado para la simulación

Simuador: Orcad Capture CIS

Participantes activos

Participantes activos en este Grupo de aprendizaje

• Anquinp (discusión)
• Adcabana (discusión)
• Guti1493 (discusión)
• WIKIUDI (discusión)

• Wikiantonio67 (discusión) 04:18 8 jun 2012 (UTC)