Pulso coseno alzado

Pulso coseno alzado

$\begin{array}{cc}& H(f)=H_{\beta }(f)*\frac{1}{R}\prod \left(\frac{f}{R}\right)\\ & H_{\beta }(f)=\frac{\pi }{4\beta }\cos \left(\frac{\pi }{2\beta }f\right)\prod \left(\frac{f}{2\beta }\right)\\ & h_{\beta }(t)={𝔽}^{-1}[H_{\beta }(f)]\to \left\{\begin{array}{cc}& \cos \left(2\pi f_{0}t\right)\underset{𝔽}{⟷}\frac{1}{2}\delta (f-f_0)+\frac{1}{2}\delta (f+f_0)\\ & \prod \left(\frac{t}{T}\right)\underset{𝔽}{⟷}T\mathrm{sinc}(Tf)\\ \end{array}\right\}\\ & \cos \left(\frac{\pi }{2\beta }f\right)=\cos \left(\frac{\pi }{2\beta }\frac{2}{2}f\right)=\cos \left(\frac{1}{4\beta }2\pi f\right)\\ & h_{\beta }(t)=\frac{\pi }{4\beta }(\frac{1}{2}\delta (t-\frac{1}{4\beta })+\frac{1}{2}\delta (t+\frac{1}{4\beta }))*2\beta \mathrm{sinc}\left(2\beta t\right)=\\ & h_{\beta }(t)=\frac{\pi }{4}(\delta (t-\frac{1}{4\beta })+\delta (t+\frac{1}{4\beta }))*\mathrm{sinc}\left(2\beta t\right)\\ & \mathrm{sinc}(Tt)=\frac{\sin \left(T\pi t\right)}{T\pi t}\\ & h_{\beta }(t)=\frac{\pi }{4}(\underset{\mathrm{sinc}(2\beta t-\frac{1}{2})}{\underbrace{\mathrm{sinc}\left(2\beta (t-\frac{1}{4\beta })\right)}}+\underset{\mathrm{sinc}(2\beta t+\frac{1}{2})}{\underbrace{\mathrm{sinc}\left(2\beta (t+\frac{1}{4\beta })\right)}})=\\ & \frac{\pi }{4}(\frac{\sin \left(2\beta \pi (t-\frac{1}{4\beta })\right)}{2\beta \pi (t-\frac{1}{4\beta })}+\frac{\sin \left(2\beta \pi (t+\frac{1}{4\beta })\right)}{2\beta \pi (t+\frac{1}{4\beta })})=\frac{\pi }{4}(\frac{\sin (2\beta \pi t-\frac{\pi }{2})}{2\beta \pi t-\frac{\pi }{2}}+\frac{\sin (2\beta \pi t+\frac{\pi }{2})}{2\beta \pi t+\frac{\pi }{2}})=\\ & \left\{\begin{array}{cc}& \sin (a\pm b)=\sin a\cos b+\sin b\cos a\to \\ & \sin (a\pm \frac{\pi }{2})=\sin a\stackrel{0}{\overbrace{\cos (\pm \frac{\pi }{2})}}+\sin (\pm \frac{\pi }{2})\cos a=\pm \cos a\\ \end{array}\right\}\\ & \frac{\pi }{4}(\frac{-\cos \left(2\beta \pi t\right)}{2\beta \pi t-\frac{\pi }{2}}+\frac{\cos \left(2\beta \pi t\right)}{2\beta \pi t+\frac{\pi }{2}})=\frac{\pi }{4}\cos \left(2\beta \pi t\right)(\frac{1}{2\beta \pi t+\frac{\pi }{2}}-\frac{1}{2\beta \pi t-\frac{\pi }{2}})=\\ & \frac{\pi }{4}\cos \left(2\beta \pi t\right)\left(\frac{(2\beta \pi t-\frac{\pi }{2})-(2\beta \pi t+\frac{\pi }{2})}{{\left(2\beta \pi t\right)}^2-{\left(\frac{\pi }{2}\right)}^2}\right)\\ \end{array}$

$\begin{array}{cc}& \frac{\pi }{4}\cos \left(2\beta \pi t\right)\left(\frac{-\pi }{{\left(2\beta \pi t\right)}^2-{\left(\frac{\pi }{2}\right)}^2}\right)=\frac{\pi }{4}\cos \left(2\beta \pi t\right)\left(\frac{\pi }{\frac{{\pi }^2}{4}-4{\beta }^2{\pi }^2{t}^2}\right)=\\ & \cos \left(2\beta \pi t\right)\left(\frac{{\pi }^2}{{\pi }^2-16{\beta }^2{\pi }^2{t}^2}\right)=\cos \left(2\beta \pi t\right)\left(\frac{1}{1-16{\beta }^2{t}^2}\right)\\ & h_{\beta }(t)=\frac{\cos \left(2\beta \pi t\right)}{1-{\left(4\beta t\right)}^2}\\ & \\ & H(f)=H_{\beta }(f)*\frac{1}{R}\prod \left(\frac{f}{R}\right)=\frac{\pi }{4\beta }\cos \left(\frac{\pi }{2\beta }f\right)\prod \left(\frac{f}{2\beta }\right)*\frac{1}{R}\prod \left(\frac{f}{R}\right)\\ & h(t)=h_{\beta }(t)\cdot \mathrm{sinc}\left(Rt\right)=\frac{\cos \left(2\beta \pi t\right)}{1-{\left(4\beta t\right)}^2}\cdot \mathrm{sinc}\left(Rt\right)\\ \end{array}$

¿Por qué otro tipo de filtro?

Para enviar datos digitales es común utilizar un pulso rectangular a modo de función “generadora”, sin embargo, esto nos da un problema en frecuencia, la transformada de Fourier de un pulso rectangular es una sinc, que tiene un ancho de banda infinito. Como el espectro es un recurso limitado, tendremos que limitar esa señal de alguna manera, con el consiguiente aumento de la probabilidad de error. Por ello, se usa la función coseno alzado que decrece mas rápidamente que la sinc conforme aumenta la frecuencia (esta mas limitada).

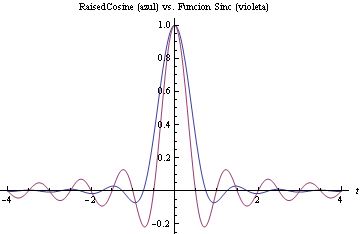
Aquí como se ve, aunque el lóbulo principal del coseno alzado sea mayor que el de la sinc, decrece mas rápidamente haciéndose prácticamente nulo en unos pocos segundos. Por ejemplo, con el ancho de banda necesario para contener el 98% de la energía en el coseno alzado, contendríamos solamente el 80% de la energía en la función Sinc.