DSB

Representación en tiempo y frecuencia

La modulación DSB o doble banda lateral es una modulación lineal analógica. Matemáticamente puede ser de las más sencillas de expresar, pues no es más que el producto de nuestra señal moduladora (la señal que contiene la información y queremos transmitir) por la portadora (encargada de mover el espectro).

$\begin{array}{cc}& c(t)=A_c\cos ({\omega }_{c}t)=A_c\cos (2\pi f_{c}t)\\ & x(t)\text{ o }{x}_m(t):\text{ Moduladora}\\ & x_{DSB}(t)=A_{c}x(t)\cos ({\omega }_{c}t)\\ \end{array}$

¿Cuál es la representación en frecuencia de una señal DSB?

$\begin{array}{cc}& x_{DSB}(t)=A_{c}x(t)\cos ({\omega }_{c}t)=A_{c}x(t)\left(\frac{e^{j{\omega }_{c}t}+e^{-j{\omega }_{c}t}}{2}\right)\\ & 𝔽[x(t)e^{+j{\omega }_{0}t}]=X(f-f_0)\\ & X_{DSB}(f)=\frac{A_c}{2}(X(f-f_c)+X(f+f_c))\\ \end{array}$

Como desplazamos el espectro de nuestra señal original a la frecuencia de la portadora, queda replicada en la parte positiva y la negativa.

Propiedades y DEP

Con la representación de señales paso-banda vista en el tema anterior, podemos obtener que:

$\begin{array}{cc}& x(t)=x_I(t)\cos ({\omega }_{c}t)-x_Q(t)\sin ({\omega }_{c}t)\\ & s(t)=x_{DSB}(t)=A_{c}x(t)\cos ({\omega }_{c}t)\\ & s_I(t)=A_{c}x(t)\\ & s_Q(t)=0\\ & e(t)=A_c|x(t)|\ne A_{c}x(t)\\ \end{array}$

¿Cuál será su DEP y su potencia?

Para ello, tendremos que calcular su autocorrelación:

$\begin{array}{cc}& R_{DSB}(\tau )=\underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\cdot \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{x}_{DSB}^{*}(t)\cdot x_{DSB}(t+\tau )\partial t=\underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\cdot \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{[A_{c}x(t)\cos ({\omega }_{c}t)]}^{*}\cdot [A_{c}x(t+\tau )\cos \left({\omega }_c(t+\tau )\right)]\partial t=\\ & \underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\cdot A_c^2\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{x}^{*}(t)x(t+\tau )\cos ({\omega }_{c}t)\cdot \cos ({\omega }_{c}t+{\omega }_c\tau )\partial t\to \{\cos a\cos b=\frac{\cos (a+b)+\cos (a-b)}{2}\}\\ & \underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\cdot A_c^2\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{x}^{*}(t)x(t+\tau )\left(\frac{\stackrel{\text{fuera del area de }\int }{\overbrace{\cos (2{\omega }_{c}t+\tau )}}+\cos ({\omega }_c\tau )}{2}\right)\partial t=\underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\cdot \frac{A_c^2}{2}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{x}^{*}(t)x(t+\tau )\stackrel{\text{No depende de t}}{\overbrace{\cos ({\omega }_c\tau )}}\partial t=\\ & \frac{A_c^2}{2}\cos ({\omega }_c\tau )\stackrel{R_x(\tau )}{\overbrace{\underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\cdot \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{x}^{*}(t)x(t+\tau )\partial t}}=\frac{A_c^2}{2}\cos ({\omega }_c\tau )R_x(\tau )\\ \end{array}$

Por lo que la DEP:

$\begin{array}{cc}& R_{DSB}(\tau )=\frac{A_c^2}{2}{R}_x(\tau )\cos ({\omega }_c\tau )\to 𝔽\to \\ & G_{DSB}(f)=\frac{A_c^2}{4}(G_x(f-f_c)+G_x(f+f_c))\\ \end{array}$

Y la potencia de la señal:

$\begin{array}{cc}& P_{DSB}=S_{DSB}=R_{DSB}(0)=\frac{A_c^2}{2}{R}_x(0)\cos ({\omega }_c\tau =0)=\\ & S_{DSB}=\frac{A_c^2}{2}{S}_x\\ \end{array}$

De las ventajas que se pueden decir de esta modulación es que toda potencia dada a la señal s(t) es usada para la información (al contrario de lo que ocurre en AM, donde parte de la potencia se la lleva la portadora), a pesar de todo, el no tener potencia en la portadora nos generará problemas en la demodulación, pudiendo únicamente utilizar demodulación coherente, que es más compleja que la de envolvente.

Relación señal a ruido de una señal DSB (detección coherente)

$\begin{array}{cc}& s(t)=A_{c}x(t)\cos ({\omega }_{c}t)\\ & s_R(t)=s(t)\cdot \frac{g_T}{L}=A_c\frac{g_T}{L}x(t)\cos ({\omega }_{c}t)\\ \end{array}$

Llamemos a $A_R=A_c\frac{g_T}{L}$ :

$s_R(t)=A_{R}x(t)\cos ({\omega }_{c}t)$

Tras el filtro de recepcion tenemos:

$\begin{array}{cc}& y_R(t)=s_R(t)+n_R(t)\\ & n_R(t)?\\ & G_n(f)=\frac{\eta }{2}\\ & G_{n_R}(f)=G_n(f)\cdot {|H_R(f)|}^2=G_n(f)\cdot (\prod \left(\frac{f-f_c}{2W}\right)+\prod \left(\frac{f+f_c}{2W}\right))\\ \end{array}$

IMAGEN MATHEMATICA

El tamaño de los filtros de recepcion como de detección tienen que ser tal que dejen pasar el ancho de banda de la señal.

En este punto, después del filtro de recepcion, calculemos la relación señal a ruido:

$\begin{array}{cc}& {\left({}^S╱{}_N\right)}_R=?\\ & R_{S_R}(\tau )=\frac{A_R^2}{2}{R}_x(\tau )\cos ({\omega }_c\tau )\\ & S_R=R_{S_R}(0)=\frac{A_R^2}{2}{S}_x\\ \end{array}$

Con el ruido, tenemos:

$N_R=R_{n_R}(\tau =0)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{G}_{n_R}(f)\partial f=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{\frac{\eta }{2}}{\underbrace{G_n(f)}}\cdot {|H_R(f)|}^2\partial f=2(\frac{\eta }{2}\cdot 2W)=2\eta W$

Por lo que, finalmente:

${\left({}^S╱{}_N\right)}_R=\frac{S_R}{N_R}=\frac{S_R}{2\eta W}=\frac{\frac{A_R^2}{2}{S}_x}{2\eta W}$

Una detalle a comentar es que, independientemente de la modulación usada o que no este modulada (banda-base) siempre tenemos que:

${\left({}^S╱{}_N\right)}_R=\frac{S_R}{N_R}=\frac{S_R}{\eta {\beta }_T}\underset{{\beta }_T=2W}{\overset{DSB}{\to }}\frac{S_R}{\eta 2W}$

Ahora bien, tras el filtro de recepcion tenemos un detector coherente que, para demodular la señal aplica un multiplicador y un filtro paso-bajo:

$\begin{array}{cc}& y_D(t)=s_D(t)+n_D(t)=y_R(t)\cos ({\omega }_{c}t)\text{ y filtrar}\\ & y_R(t)=s_R(t)+n_R(t)\to \\ & s_D(t)\to s_R(t)\cos ({\omega }_{c}t)=(A_{R}x(t)\cos ({\omega }_{c}t))\cos ({\omega }_{c}t)=A_{R}x(t)\left(\frac{1+\stackrel{\text{Lo elimina el filtro paso-bajo}}{\overbrace{\cos (2{\omega }_{c}t)}}}{2}\right)\\ & s_D(t)=\frac{A_R}{2}x(t)\\ & n_R(t).\cos ({\omega }_{c}t)=???\\ \end{array}$

Directamente no sabemos resolver cuanto vale el ruido, pero para ello hemos definido las representación paso-banda de las señales:

$\begin{array}{cc}& x(t)=x_I(t)\cos ({\omega }_{c}t)-x_Q(t)\sin ({\omega }_{c}t)\to \\ & n(t)=n_I(t)\cos ({\omega }_{c}t)-n_Q(t)\sin ({\omega }_{c}t)\to \\ & n_R(t)=n_{R_I}(t)\cos ({\omega }_{c}t)-n_{R_Q}(t)\sin ({\omega }_{c}t)\\ \end{array}$

$\begin{array}{cc}& y_R(t)=s_R(t)+n_R(t)=s_R(t)+n_{R_I}(t)\cos ({\omega }_{c}t)-n_{R_Q}(t)\sin ({\omega }_{c}t)\\ & y_R(t).\cos \left({\omega }_{c}t\right)\text{ y filtrar}\\ & n_D(t)=n_R(t)\cdot \cos ({\omega }_{c}t)\\ & n_D(t)=(n_{R_I}(t)\cos ({\omega }_{c}t)-n_{R_Q}(t)\sin ({\omega }_{c}t))\cdot \cos ({\omega }_{c}t)\to \left\{\begin{array}{cc}& \cos a\cos b=\frac{\cos (a+b)+\cos (a-b)}{2}\\ & \sin a\cos b=\frac{\sin (a+b)+\sin (a-b)}{2}\\ \end{array}\right\}\\ & n_D(t)=n_{R_I}(t)\left(\frac{\stackrel{\text{eliminado por el filtro}}{\overbrace{\cos (2{\omega }_{c}t)}}+1}{2}\right)-n_{R_Q}(t)\left(\frac{\stackrel{\text{eliminado por el filtro}}{\overbrace{\sin (2{\omega }_{c}t)}}+0}{2}\right)\\ & n_D(t)=\frac{n_{R_I}(t)}{2}\\ \end{array}$

Por lo que finalmente,

$\begin{array}{cc}& y_D(t)=s_D(t)+n_D(t)=\frac{A_{R}x(t)}{2}+\frac{n_{R_I}(t)}{2}\\ & G_{Y_D}(f)=\underset{T\to \mathrm{\infty }}{\lim }\frac{{|Y_D(f)|}^2}{T}\to P_Y=\frac{A_R^2}{4}{S}_x+\frac{N_{R_I}}{4}\to \{\text{Propiedades: }{S}_x=S_{x_I}=S_{x_Q}\}\\ & P_Y=\frac{A_R^2}{4}{S}_x+\frac{N_R}{4}\to \{N_R=2\eta W\}\\ & {\left({}^S╱{}_N\right)}_D=\frac{S_D}{N_D}=\frac{\frac{A_R^2}{4}{S}_x}{\frac{N_R}{4}}=\frac{A_R^2{S}_x}{N_R}=\frac{A_R^2{S}_x}{2\eta W}\\ & S_R=\frac{A_R^2}{2}{S}_x\to {\left({}^S╱{}_N\right)}_D=\frac{A_R^2{S}_x}{2\eta W}=\frac{S_R}{\eta W}\\ \end{array}$

Comparación mediante factor de calidad

Para comparar lo buena que es nuestra relación señal a ruido (para saber como de buena es nuestra modulación), lo comparamos con el factor de calidad, que no es mas que la relación señal a ruido que obtendriamos en banda base, esto es, sin modular la señal:

$\gamma =\frac{S_R}{\eta W}\to {\left({}^S╱{}_N\right)}_D=\gamma$

¿Por qué no podemos usar detección por envolvente?

Para nuestra DSB, teníamos que la envolvente era: $e(t)=A_c|x(t)|\ne A_{c}x(t)$

Si dibujamos nuestra señal Double Side Band, junto con la moduladora para ver la envolvente, vemos que:

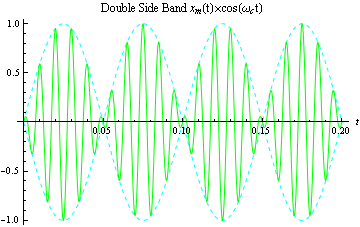
Debido a que el modulo de la moduladora no es igual a la moduladora, no podemos usar la demodulación por envolvente, que presenta ventajas como su facilidad y alta calidad:

En caso de que usásemos un demodulador por envolvente, la señal a la salida seria: