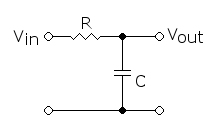
Circuito RC

Se considera un circuito RC a todo aquel circuito compuesto por: de una parte, una asociación de resistencias, y de otra, un único condensador (se incluyen los casos en que el hay varios capacitores -condensadores- que se pueden reducir a uno equivalente), puede tener también fuentes tanto dependientes como independientes.

Cualquier variable X del circuito tiene una solución de la solución (forma)

                                   $X=A{e}^{(\frac{-t}{\tau })}$

donde

 -$\tau$(tau)=constante de tiempo = C*$R_{equ}$ donde $R_{equ}$ es la resistencia equivalente 
   vista por las placas del condensador

 -A se calcula con las condiciones iniciales del circuito

En el caso de que haya fuentes dependientes en el circuito, se hace necesario usar una fuente expiatoria para saber el valor de la $R_{equ}$ para poder hallar el $\tau$.

Cálculo de $R_{equ}$ mediante Fuente Expiatoria

Procedimiento:

Se inactiva el circuito, se reemplaza el capacitor por una fuente de valor conocido, por ejemplo reemplazamos por una fuente de 1v, y entonces hallamos la corriente que pasa por esa fuente.

Si en cambio colocamos una fuente de corriente de valor desconocido, hallamos el voltaje entre los nodos de la fuente.

Después encontramos la resistencia para el cálculo de $\tau$, (la cual "ve" el condensador entre sus bornes, que viene dada por el Teorema de Thévenin) que se calcula como $R_{equ}$ = $R_{th}=V/I$

Desarrollo matemático de las respuestas de un circuito RC

Respuesta de un circuito RC a un escalón de tensión

Como ya sabemos, la entrada en escalón corresponde a un paso brusco de tensión desde nulo a un valor determinado.
$u_c(0)=0$

Ecuación diferencial

Schéma 1

De acuerdo con el principio de superposición de tensiones, $E=u_R+u_c$

y según la ley de Ohm, $u_R=Ri$

por tanto $E=Ri+u_c$

Por otro lado, por definición: $i=\frac{dq}{dt}$ et $q=C{u}_c$

y por tanto $i=\frac{d(C{u}_c)}{dt}=C\frac{d{u}_c}{dt}$

Es por eso que $E=RC\frac{d{u}_c}{dt}+u_c$

Ecuación diferencial del circuito RC

$\frac{E}{RC}=\frac{d{u}_c}{dt}+\frac{1}{RC}{u}_c$

Solución

La solución de esta ecuación diferencial es de la forma $u_c(t)=A{e}^{-kt}+B$

• cuando $t\to \mathrm{\infty },u_c=B$ de donde $B=E$
  
  
• cuando $t=0$, $u_c(0)=0=A+B$ de donde $A=-B=-E$
  
  
• $\frac{d(-E{e}^{-kt}+E)}{dt}+\frac{1}{RC}(-E{e}^{-kt}+E)=\frac{E}{RC}$
  
  

$\Rightarrow -k(-E{e}^{-kt})+\frac{1}{RC}(-E{e}^{-kt}+E)=\frac{E}{RC}$

$⟺-k(-E{e}^{-kt})+\frac{1}{RC}(-E{e}^{-kt})+\frac{E}{RC}=\frac{E}{RC}$

$⟺-E{e}^{-kt}(-k+\frac{1}{RC})=0$

El cual presenta valores para todo el rango de t, y particularmente para t = 0 por tanto $-k+\frac{1}{RC}=0$ y $k=\frac{1}{RC}$

• Solución de la ecuación diferencial:
  

La tensión en bornes del condensador en función del tiempo :
$u_c(t)=-E{e}^{-kt}+E$

$u_c(t)=E(1-e^{-\frac{t}{RC}})$

Constante de tiempo del circuito RC

Expresión y análisis dimensional básico

Si de nuevo hacemos $\tau$ (tau) de modo que ^{$\tau =R.C$} Buscamos las dimensiones físicas de $\tau$ :

$R=\frac{u}{i}=\frac{[V]}{[A]}$    et    $C=\frac{q}{u}=\frac{i.t}{u}=\frac{[A].[s]}{[V]}$

o    $\tau =R.C$    entonces    $\tau =\frac{[V].[A].[s]}{[A].[V]}$

$\Rightarrow$ $\tau =[s]$

El producto $R.C$ es por tanto un tiempo. En unidades , $\tau$ se expresa en segundos. A esta constante se le denomina " Constante de tiempo del circuito RC ".

Cálculo de la constante de tiempo

• Trazar la curva de la tensión en bornes del condensador en función del tiempo durante la carga.
• Trazar una recta de valor de la ordenada igual a la carga máxima($u_{max}$) del condensador.
• Trazar una recta, partiendo del origen de la curva y tangente a la curva en ese mismo punto.
• El punto de intersección de estas dos rectas tiene como abscisa de tiempo el valor $\tau$ y en esta abscisa el valor de la ordenada vale $(1-e^{-1})u_{max}$ que coincide aproximadamente con $0,63u_{max}$

durante la carga de un condensador a través de una resistencia $R$, bajo una tensión $E$ del generador, constante :

• En el instante $t=\tau$, $u_C=0,63E$
• Y en el instante $t=5\tau$, $u_C=0,99E$ (El condensador está prácticamente cargado)

Descarga de un condensador a través de una resistencia

$u_c(0)=E(fuente)$

==== Planteamiento de la ecuación diferencial

====

Según el principio de superposición de tensiones, $u_R+u_c=0$
O $u_R=Ri$ y $i=\frac{dq}{dt}=\frac{d(C{u}_c)}{dt}=C\frac{d{u}_c}{dt}$
Podemos sustituir: $RC\frac{d{u}_c}{dt}+u_c=0$
Sea

$\frac{d{u}_c}{dt}+u_c\frac{1}{RC}=0$

Utilidad

Los circuitos RC tienen una función inmediata de temporizadores, aprovechando su constante de tiempo con dimensiones de segundos. Pero, por otra parte, su uso fundamental es como filtros: bien paso alto, que corta las frecuencias bajas; bien paso bajo, que corta las frecuencias altas, lo cual depende de la posición de montaje del condensador.

Existe una frecuencia específica, la llamada frecuencia de corte, en la cual la reactancia capacitiva es igual a la resistencia. (También ocurre un desfase asociado de 45 grados, obvio al ver los fasores.)

$R=X_c$

Sustituyendo $X_C=\frac{1}{2\pi fC}$ encontramos que:

$R=\frac{1}{2\pi fC}$

La frecuencia de corte, definida como la frecuencia a la que la potencia de la señal se atenúa al 30% (o 3.01 dB), es una función de los valores de resistencia y capacidad. Podemos operar en la fórmula anterior para resolver $f$ de la siguiente forma:

$f_{corte}=\frac{1}{2\pi RC}$

Filtro paso bajo

Cuando el condensador queda en paralelo con la carga ,mientras la resistencia queda en serie tanto con toda la salida, incluido el condensador, el filtro creado es de paso bajo.

Filtro paso alto

Cuando la resistencia está en paralelo con la carga y el condensador en serie con el montaje incluida la resistencia, el filtro creado es de paso alto.

Un circuito simple RC crea un filtro con una atenuación de pendiente 20.0 dB/década, o bien 6.02 dB/octava.