PSK

PSK (Phase Shift Keying)

$\begin{array}{cc}& s_{PSK}(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}p(t-k{T}_s)\cos ({\omega }_{c}t+{\phi }_k)=\\ & A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}p(t-k{T}_s)\cos \left({\omega }_{c}t\right)\underset{I_k}{\underbrace{\cos \left({\phi }_k\right)}}-A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}p(t-k{T}_s)\sin \left({\omega }_{c}t\right)\underset{Q_k}{\underbrace{\sin \left({\phi }_k\right)}}\\ & {\cos }^{2}x+{\sin }^{2}x=1\to \\ & I_k^2+Q_k^2=1\\ \end{array}$

Dependiendo del numero de niveles tenemos diferentes tipos de PSK

BPSK (Binary Phase Shift Keying)

Tambien llamada PRK (Phase Reversal Keying).

Constellation diagram for BPSK.

$\begin{array}{cc}& s_{BPSK}(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}p(t-k{T}_s)\cos ({\omega }_{c}t+{\phi }_k)=\\ & {\phi }_k=\{0,\pi \}\to s_{BPSK}(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}p(t-k{T}_s)\cos \left({\omega }_{c}t\right)\underset{I_k}{\underbrace{\cos \left({\phi }_k\right)}}\\ \end{array}$

${\phi }_k$	$I_k$
$0$	$+1$
$\pi$	$-1$

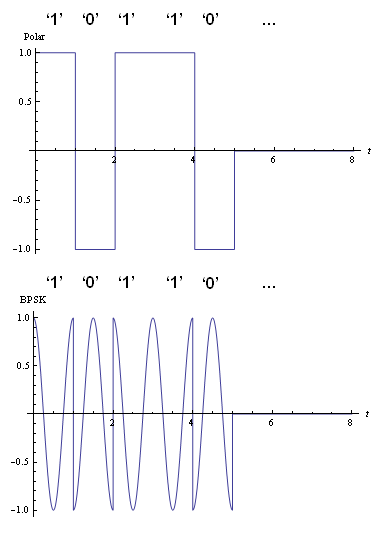
Por lo que vemos, para este caso particular de PSK, la señal puede ser modelada como una codificacion polar modulada por un coseno

$\begin{array}{cc}& x_{BPSK}(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{I}_k\cdot p(t-k{T}_s)\cos \left({\omega }_{c}t\right)\\ & x_I(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{I}_k\cdot p(t-k{T}_s),x_Q(t)=0\\ & {\overline{G}}_I(f)=G_{polar}(f)=A^2{T}_s{\mathrm{sinc}}^2\left(T_{s}f\right)\\ & G_x(f)=\frac{G_I(f-f_c)+G_I(f+f_c)}{4}+\frac{G_Q(f-f_c)+G_Q(f+f_c)}{4}\to \\ & G_x(f)=\frac{G_I(f\pm f_c)}{4}\to \\ & G_{x_{BPSK}}(f)=\frac{A^2{T}_s{\mathrm{sinc}}^2\left(T_s(f\pm f_c)\right)}{4}\\ \end{array}$

Para la probabilidad de error (BER):

BER de BPSK

QPSK (Quadrature Phase Shift Keying)

$\begin{array}{cc}& s_{PSK}(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}p(t-k{T}_s)\cos ({\omega }_{c}t+{\phi }_k)=\\ & A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}p(t-k{T}_s)\cos \left({\omega }_{c}t\right)\underset{I_k}{\underbrace{\cos \left({\phi }_k\right)}}-A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}p(t-k{T}_s)\sin \left({\omega }_{c}t\right)\underset{Q_k}{\underbrace{\sin \left({\phi }_k\right)}}\\ \end{array}$

Existe más de un tipo de QPSK, la que se utiliza en la práctica:

Constellation diagram for QPSK with Gray coding. Each adjacent symbol only differs by one bit.

${\phi }_k$	$I_k$	$Q_k$
$+{}^{\pi }╱{}_4$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$
$+{}^{3\pi }╱{}_4$	$-\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$
$-{}^{3\pi }╱{}_4$	$-\frac{1}{\sqrt{2}}$	$-\frac{1}{\sqrt{2}}$
$-{}^{\pi }╱{}_4$	$\frac{1}{\sqrt{2}}$	$-\frac{1}{\sqrt{2}}$

$\begin{array}{cc}& s_{QPSK}(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{I}_k\cdot p(t-k{T}_s)\cos \left({\omega }_{c}t\right)-A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{Q}_k\cdot p(t-k{T}_s)\sin \left({\omega }_{c}t\right)\\ & s_I(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{I}_k\cdot p(t-k{T}_s)\\ & s_Q(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{Q}_k\cdot p(t-k{T}_s)\\ \end{array}$

Ahora, para sacar la densidad espectral de potencia:

$\begin{array}{cc}& s_I(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{I}_k\cdot p(t-k{T}_s)\to \\ & I_k=\{\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\}\\ & {\overline{G}}_x(f)={\sigma }_{a_k}^2\cdot R_s{|P(f)|}^2+m_{a_k}^2\cdot R_s^2\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{|P(k{R}_s)|}^2\delta (f-k{R}_s)\\ & {|P(f)|}^2=T_s^2{\mathrm{sinc}}^2\left(T_{s}f\right)\\ & m_{I_k}=\frac{1}{\sqrt{2}}\cdot \frac{1}{4}+(-\frac{1}{\sqrt{2}})\cdot \frac{1}{4}+(-\frac{1}{\sqrt{2}})\cdot \frac{1}{4}+\frac{1}{\sqrt{2}}\cdot \frac{1}{4}=0\\ & P_{I_k}={\left(\frac{1}{\sqrt{2}}\right)}^2\cdot \frac{1}{4}+{(-\frac{1}{\sqrt{2}})}^2\cdot \frac{1}{4}+{(-\frac{1}{\sqrt{2}})}^2\cdot \frac{1}{4}+{\left(\frac{1}{\sqrt{2}}\right)}^2\cdot \frac{1}{4}=\frac{1}{2}\\ & {\sigma }_{I_k}^2=P_{I_k}-m_{I_k}^2=\frac{1}{2}\\ & {\overline{G}}_x(f)={\sigma }_{a_k}^2\cdot R_s{|P(f)|}^2+\underset{0}{\underbrace{m_{a_k}^2}}\cdot R_s^2\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{|P(k{R}_s)|}^2\delta (f-k{R}_s)=\underset{{\left({}^1╱{}_2\right)}^2}{\underbrace{{\sigma }_{a_k}^2}}\cdot R_s\cdot T_s^2{\mathrm{sinc}}^2\left(T_{s}f\right)=\\ & {\overline{G}}_I(f)=A_c^2{\sigma }_{a_k}^2{T}_s{\mathrm{sinc}}^2\left(T_{s}f\right)=\frac{A_c^2}{2}{T}_s{\mathrm{sinc}}^2\left(T_{s}f\right)\\ \end{array}$

$\begin{array}{cc}& s_Q(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{Q}_k\cdot p(t-k{T}_s)\to \\ & Q_k=\{\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\}\to m_{a_k}=0,{\sigma }_{a_k}^2=\frac{1}{2}\\ & m_{Q_k}=\frac{1}{\sqrt{2}}\cdot \frac{1}{4}+\frac{1}{\sqrt{2}}\cdot \frac{1}{4}+(-\frac{1}{\sqrt{2}})\cdot \frac{1}{4}+(-\frac{1}{\sqrt{2}})\cdot \frac{1}{4}=0\\ & P_{Q_k}={\left(\frac{1}{\sqrt{2}}\right)}^2\cdot \frac{1}{4}+{\left(\frac{1}{\sqrt{2}}\right)}^2\cdot \frac{1}{4}+{(-\frac{1}{\sqrt{2}})}^2\cdot \frac{1}{4}+{(-\frac{1}{\sqrt{2}})}^2\cdot \frac{1}{4}=\frac{1}{2}\\ & {\sigma }_{Q_k}^2=P_{Q_k}-m_{Q_k}^2=\frac{1}{2}\\ & {\overline{G}}_Q(f)=A_c^2{\sigma }_{a_k}^2{T}_s{\mathrm{sinc}}^2\left(T_{s}f\right)=\frac{A_c^2}{2}{T}_s{\mathrm{sinc}}^2\left(T_{s}f\right)\\ \end{array}$

$\begin{array}{cc}& m_{I_k}=m_{Q_k}=0\\ & {\sigma }_{I_k}^2={\sigma }_{Q_k}^2=\frac{1}{2}\\ & {\overline{G}}_I(f)={\overline{G}}_Q(f)=A_c^2{\sigma }_{a_k}^2{T}_s{\mathrm{sinc}}^2\left(T_{s}f\right)=\frac{A_c^2}{2}{T}_s{\mathrm{sinc}}^2\left(T_{s}f\right)\\ & G_x(f)=\frac{G_I(f-f_c)+G_I(f+f_c)}{4}+\frac{G_Q(f-f_c)+G_Q(f+f_c)}{4}\to \\ & G_{QPSK}(f)=2\frac{G_{I/Q}(f-f_c)+G_{I/Q}(f+f_c)}{4}=\frac{G_{I/Q}(f\pm f_c)}{2}=\frac{A_c^2}{4}{T}_s{\mathrm{sinc}}^2\left(T_s(f\pm f_c)\right)\\ \end{array}$

Para la probabilidad de error (BER):

BER de QPSK

Existe otro tipo de QPSK:

4PSK

${\phi }_k$	$I_k$	$Q_k$
$0$	$+1$	$0$
${}^{\pi }╱{}_2$	$0$	$+1$
$\pi$	$-1$	$0$
$-{}^{\pi }╱{}_2$	$0$	$-1$

$\begin{array}{cc}& s_Q(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{I}_k\cdot p(t-k{T}_s)\to \\ & I_k=\{+1,0,-1,0\}\\ & m_{a_k}=+1\cdot \frac{1}{4}+0\cdot \frac{1}{4}+(-1)\cdot \frac{1}{4}+0\cdot \frac{1}{4}=0\\ & P_{a_k}=+1^2\cdot \frac{1}{4}+0\cdot \frac{1}{4}+{(-1)}^2\cdot \frac{1}{4}+0\cdot \frac{1}{4}=\frac{1}{2}\\ & {\sigma }_{a_k}^2=P_{a_k}-m_{a_k}^2=\frac{1}{2}\\ & s_Q(t)=A_c\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{Q}_k\cdot p(t-k{T}_s)\to \\ & Q_k=\{0,+1,0,-1\}\\ & m_{a_k}=0\cdot \frac{1}{4}+1\cdot \frac{1}{4}+0\cdot \frac{1}{4}+(-1)\cdot \frac{1}{4}=0\\ & P_{a_k}=0\cdot \frac{1}{4}+1^2\frac{1}{4}+0\cdot \frac{1}{4}+{(-1)}^2\cdot \frac{1}{4}=\frac{1}{2}\\ & {\sigma }_{a_k}^2=P_{a_k}-m_{a_k}^2=\frac{1}{2}\\ \end{array}$

$G_{4PSK}(f)=\frac{A_c^2}{4}{T}_s{\mathrm{sinc}}^2\left(T_s(f\pm f_c)\right)$

Para la probabilidad de error (BER):

BER de 4PSK

Como consecuencia final, vemos que la media y varianza de una señal PSK es constante:

$\begin{array}{cc}& m_{I_k}=m_{Q_k}=0\\ & {\sigma }_{I_k}^2={\sigma }_{Q_k}^2=\frac{1}{2}\\ \end{array}$

8-PSK,16-PSK…

Como se ha visto, la media y varianza de la señal no cambia, por lo que la densidad espectral de potencia será siempre igual independientemente del número de símbolos usados:

$G_{PSK}(f)=\frac{A_c^2}{4}{T}_s{\mathrm{sinc}}^2\left(T_s(f\pm f_c)\right)$

Constellation diagram for 8-PSK with Gray coding.

Para la probabilidad de error (BER):

BER de M-PSK

OQPSK

Signal doesn't cross zero, because only one bit of the symbol is changed at a time

π/4–QPSK

Dual constellation diagram for π/4-QPSK. This shows the two separate constellations with identical Gray coding but rotated by 45° with respect to each other.

Plantilla:Navegación