Revisión actual - 06:38 9 ago 2015
Sabemos que:
Ahora que sabemos la DEP de una señal digital ...
Codificación Unipolar NRZ


Para la probabilidad de error (BER):
Unipolar NRZ
Codificación Unipolar RZ
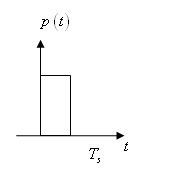

Para la probabilidad de error (BER):
Unipolar RZ
Codificación Polar


Para la probabilidad de error (BER):
Polar
Codificación Bipolar


Para la probabilidad de error (BER):
Bipolar
Codificación Manchester
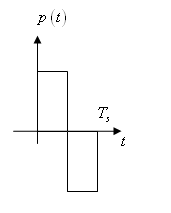

Para la probabilidad de error (BER):
Manchester
Plantilla:Navegación









